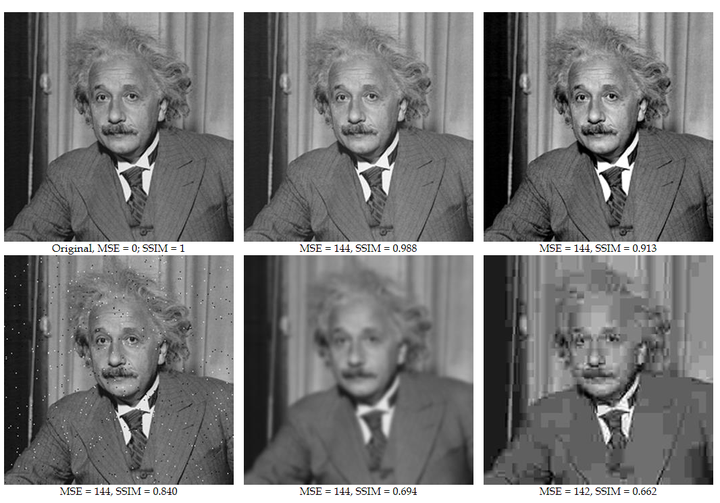A Survey on 3D Gaussian Splatting
3D Gaussian splatting (3D GS) has recently emerged as a transformative technique in the explicit radiance field and computer graphics landscape. This innovative approach, characterized by the...

https://arxiv.org/abs/2401.03890

Background
- 场景重建:涉及从图像或其他数据的集合创建场景的3D模型。
- 渲染:是一个更具体的术语,专注于将计算机可读信息(例如,场景中的3D对象)转换为基于像素的图像。
- 神经渲染:神经渲染将深度学习与传统图形技术相结合,以创建照片级真实感图像。早期的尝试使用卷积神经网络(CNNs)来估计混合权重或纹理空间解决方案。
- 辐射场:表示一个函数,该函数描述了通过空间中每个点在每个方向上传播的光量。NeRFs使用神经网络对辐射场进行建模,从而实现详细逼真的场景渲染。
- 体积表示:体积表示不仅将目标和场景建模为曲面,还将其建模为填充了材质或空白空间的体积。这种方法可以更准确地渲染雾、烟或半透明材料等现象。
- Ray-Marching:是一种与体积表示一起使用的技术,通过增量跟踪穿过体积的光的路径来渲染图像。NeRF分享了体积射线行进的相同精神,并引入了重要性采样和位置编码来提高合成图像的质量。在提供高质量结果的同时,体积射线行进在计算上是昂贵的,这促使人们寻找更有效的方法,如3D GS。
- 基于点的渲染:基于点的渲染是一种使用点而不是传统多边形来可视化3D场景的技术。这种方法对于渲染复杂、非结构化或稀疏的几何数据特别有效。点可以用额外的属性来增强,如可学习的神经描述符,并有效地渲染,但这种方法可能会遇到诸如渲染中的漏洞或混叠效应等问题。3D GS通过使用各向异性高斯来扩展这一概念,以实现场景的更连续和更有凝聚力的表示。
Overview
- 辐射场:辐射场是三维空间中光分布的表示,它捕捉光如何与环境中的表面和材料相互作用。从数学上讲,辐射场可以描述为函数,其中将空间中的一个点和由球面坐标指定的方向映射到非负辐射值。辐射场可以通过隐式或显式表示进行封装,每种表示都具有特定的场景表示和渲染优势。
- 隐式辐射场:隐式辐射场表示场景中的光分布,而不明确定义场景的几何体。在深度学习时代,它经常使用神经网络来学习连续的体积场景表示。最突出的例子是NeRF。在NeRF中,MLP网络用于将一组空间坐标和观看方向映射到颜色和密度值。任何点的辐射度都不是明确存储的,而是通过查询神经网络实时计算的。因此,函数可以写成:
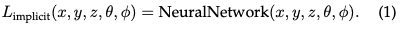
这种格式允许对复杂场景进行可微分和紧凑的表示,尽管由于体积光线行进,渲染过程中的计算负载往往很高。
- 显式辐射场:相反,显式辐射场直接表示离散空间结构中的光分布,例如体素网格或点集。该结构中的每个元素存储其在空间中的相应位置的辐射信息。这种方法允许更直接且通常更快地访问辐射数据,但代价是更高的内存使用率和潜在的更低分辨率。显式辐射场表示的一般形式可以写成:
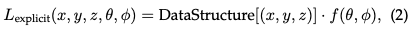
其中DataStructure可以是网格或点云,是基于观看方向修改辐射的函数。
- 两全其美的3D Gaussian Splatting:3D GS表示从隐式辐射场到显式辐射场的转变。它通过利用3D高斯作为灵活高效的表示,利用了这两种方法的优势。这些高斯系数经过优化,可以准确地表示场景,结合了基于神经网络的优化和显式结构化数据存储的优点。这种混合方法旨在通过更快的训练和实时性能实现高质量渲染,特别是对于复杂的场景和高分辨率输出。3D高斯表示公式化为:
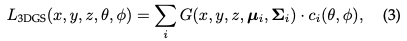
传统方法
早期的技术基于光场生成逼真的图像,后期
- structure-from-motion(SfM)
- MultiView Stereo多视图立体(MVS)算法
通过从图像序列估计3D结构进一步推进了这一领域。
典型的神经场算法在视觉计算中如下:
- 通过时空采样坐标并把它们送入神经网络产生预测的重建场量。
- 应用前向地图将重建场量与传感器域(如RGB图像)对应起来,计算重建误差。
NeRF-Based, 2020
- 通过隐式建模将场景建模为连续的辐射场,任何点的辐射度都不是明确存储的,而是通过查询神经网络实时计算的。因此可以实现任意分辨率的建模和渲染
- 通过为每个3D位置分配一个密度值来提升透明半透明物体的渲染能力
NeRF的局限性,主要包括:- 计算成本高:任何点的辐射度都不是明确存储的,而是通过输入至神经网络实时计算的。
- 处理反射和透明度复杂的物体困难:虽然
NeRF可以处理一些反射和透明度的效果,但对于具有复杂反射和透明度的物体
- 需求高质量的输入数据训练且训练时间长
一文详解 | 你还没了解NeRF 神经辐射场吗?
微信号
cv3derNews

https://mp.weixin.qq.com/s?__biz=MzkyMTUwMTU5Mg==&mid=2247484754&idx=1&sn=b95863155ecf7a7537cd45836598925e&chksm=c183efa5f6f466b3c63d2a4d0dbaca076ac1148c76c8cab58365471823c06339c0c11bed9496&token=752429925&lang=zh_CN#rd

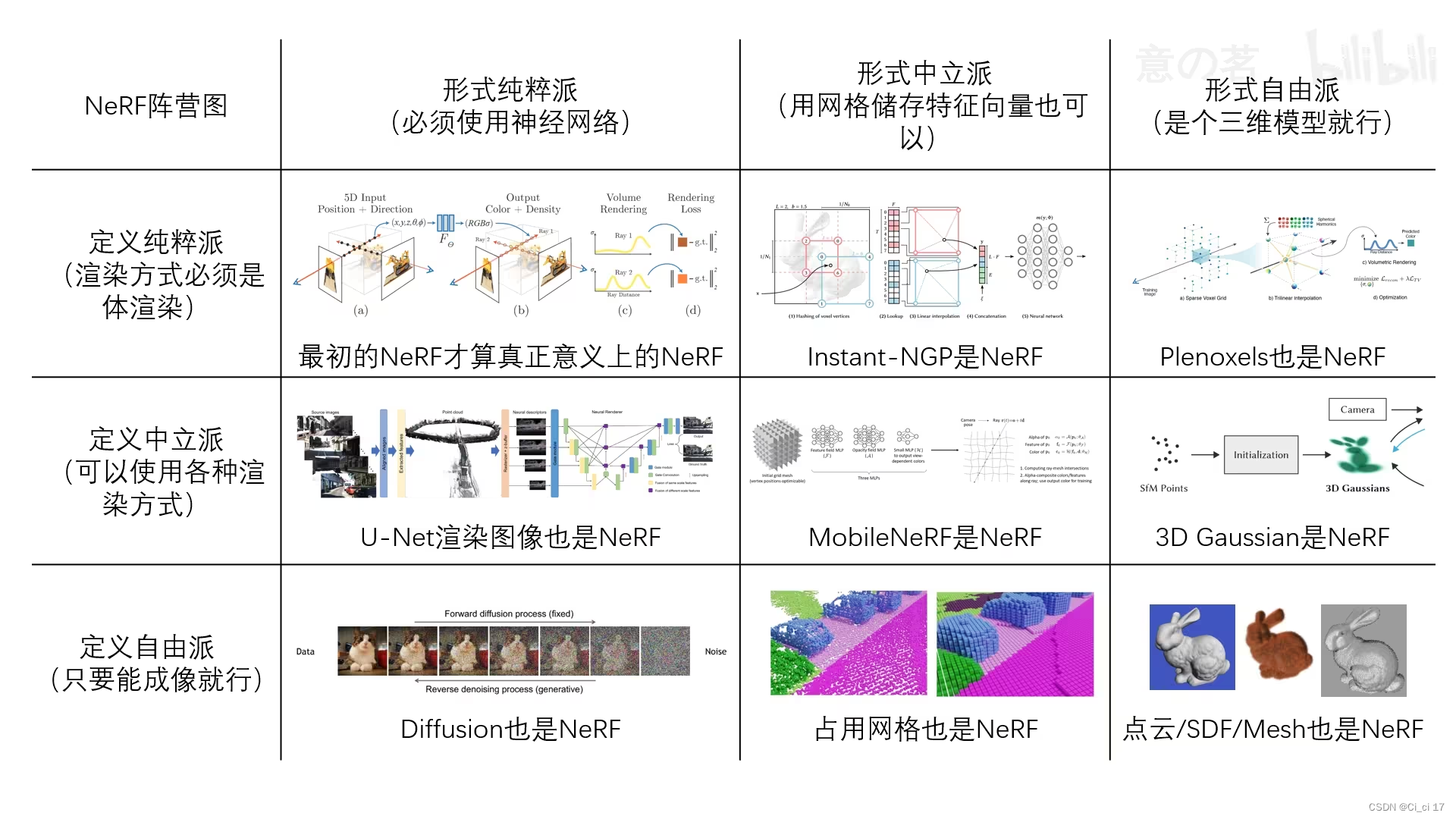
3D Gaussian Splatting 抛雪球
- 结合隐式(不明确定义场景几何体,对场景中的光/材质分布等建模)和显式(对空间中每个位置的信息建模)辐射场。
- 输入:考虑一个由(数百万)优化的3D高斯表示的场景。
- 投影到基于像素的图像平面上:splatting
- 排序,并计算每个像素的值。
- 3D GS的核心是一个优化过程,旨在构建大量的3D高斯集合,准确捕捉场景的本质,从而促进自由视点渲染。
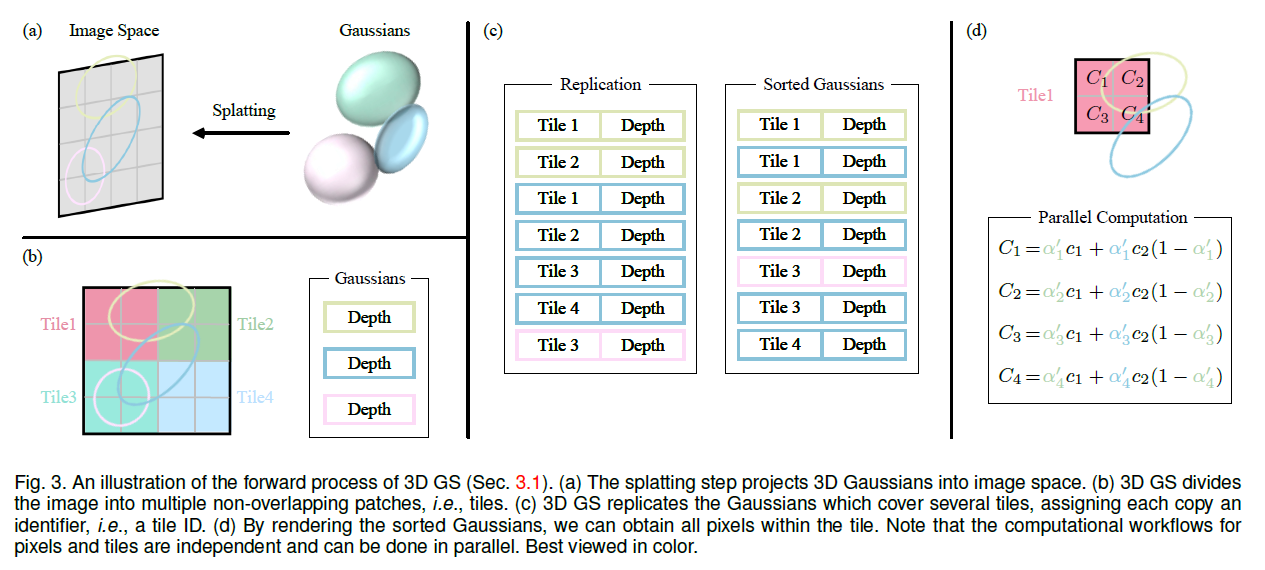
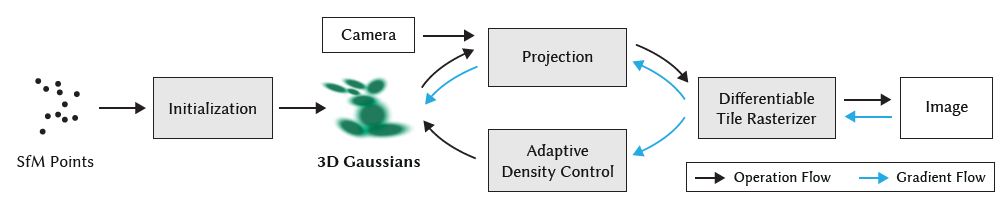
3D Gaussian Splatting中的数学推导
此文记录个人学习过程,如有错误欢迎私信交流,十分感谢!(第一次在知乎发blog,紧张。) 3D Gaussian Splatting,简记为3DGS,是一种很有希望的场景表达方式。我在YouTube冲浪相关视频时,看到了这样一段评论: …

https://zhuanlan.zhihu.com/p/666465701

一文带你入门 3D Gaussian Splatting
强烈去看 b 站 up 主中恩实验室的系列视频! Siggraph 2023 Best Paper!1. 引言1.1 任务文章涉及到的任务是三维重建+渲染。 文章提出了一种新方法实现了辐射场的实时渲染,能够在较少的训练时间中,实现SOTA级别…

https://zhuanlan.zhihu.com/p/680669616

开始弃用NeRF?为什么Gaussian Splatting在自动驾驶场景如此受欢迎?
本文经自动驾驶之心公众号授权转载,转载请联系出处。写在前面&笔者的个人理解三维 Gaussian splatting(3DGS)是近年来在显式辐射场和计算机图形学领域出现的一种变革性技术。这种创新方法的特点是使用了数百万个3D高斯,这与神经辐射场(NeRF)方法有很大的不同,后者主要使用隐式的基于坐标的模型将空间坐标映射到像素值..

https://www.gfkjgy.com/cms/show-3671.html
Data
数据集包含,
- Image:场景图片,一组从不同视角拍摄的场景照片,groundtruth
- Camera extrinsic:每张照片的坐标变换(3D世界坐标 to 3D相机坐标 to 2D图像平面坐标)信息(q、t),3D to 3D可逆,3D to 2D不可逆变换,因为缺少了深度信息
qvec=array([0.99498316,−0.06155189,−0.07766309,0.01372295]),tvec=array([2.53346241,0.75862732,4.52239219])
- Camera intrinsic:内参,所有图像共享,完成2D图像平面坐标 to 2D传感器坐标的坐标变换,可逆。
model=′PINHOLE′,width=1959,height=1090,params=array([1159.5880733,1164.66012875,979.5,545.])
Preprocess
Transformation
- Overall, 从目标的世界坐标系3D,转换到相机坐标系3D,然后转换到图像平面坐标系2D(图像物理坐标),最后转换到传感器坐标系2D(图像像素坐标)。转换的矩阵关系为(world 2 camera 2 image 2 sensor coordinate system):
[xs ys 1]T=HisHciHwc[X Y Z 1]T - 首先,world 2 camera,都是3D坐标系,可逆的刚体变换,包含平移和旋转变换,6个自由度(X0,Y0,Z0,α,β,γ)
- 用齐次坐标的形式表示,给每个坐标点增加一维坐标,能非常方便的表达点在直线或平面上,点坐标与法向量的内积为零
xcyczc1=[R03TX01]xwywzw1=Wxwywzw1
Hwc=[R03TX01]R=RX(α)RY(β)RZ(γ)Rpitch=RX(α)=1000cosαsinα0−sinαcosαRyaw=RY(β)=cosβ0−sinβ010sinβ0cosβRroll=RZ(γ)=cosγsinγ0−sinγcosγ0001
- camera 2 image,在x和y方向是重合的,只是z轴的缩放,根据针孔成像原理,通过焦距focal length控制缩放,并写成齐次坐标的形式。
xi=fxc/zcyi=fyc/zczcxiyi1=f000f0001000xcyczc1 - image 2 sensor,传感器坐标系的初始原点一般不是平面的中心点。有一个小的位移,一般还包括了剪切和尺度的变换。
xs=xi/dx+x0ys=yi/dy+y0xsys1=1/dx0001/dy0x0y01xiyi1
- 因此,汇总可得,从世界坐标空间到图像像素空间(sensor space)的相机坐标变换表示为
zcxsys1=1/dx0001/dy0x0y01f000f0001000[R03TX01]xwywzw1=1/dx0001/dy0x0y01f000f0001000Wxwywzw1
(四十)通俗易懂理解——相机坐标转换
首先要弄清相机坐标的转换关系。一、世界坐标系(world coordinate),也称为测量坐标系,是一个三维直角坐标系,以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。 坐标…

https://zhuanlan.zhihu.com/p/90295867
最本质的相机内参intrinsics与外参extrinsics分析,从建模,推导到求解_intrinsic camera-CSDN博客
文章浏览阅读6.1k次,点赞17次,收藏38次。本文从最本质的原理出发,对相机的外参和内参进行了描述。从不同坐标系的建模,到3D到2D的投影矩阵分析,到矩阵变换的求解。全面的分析和描述了相机参数的原理。camera extrinsics and intrinsics。_intrinsic camera

https://blog.csdn.net/qq_32998593/article/details/105628305
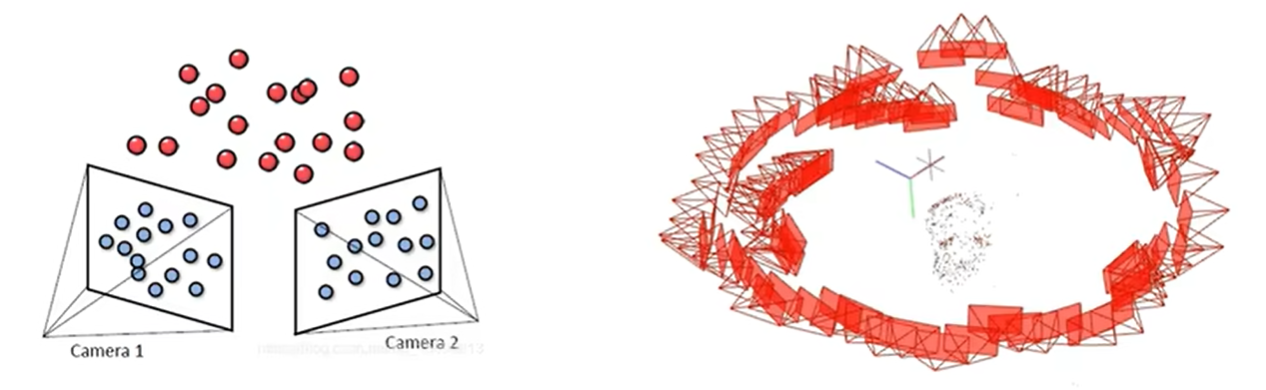
SfM initialization, Structure from Motion
可以直接调用 COLMAP 库来完成这一步,当无法获得点云时,可以使用随机初始化来代替,但可能会降低最终的重建质量和收敛速度。SfM 初始化点云过程的主要步骤如下:
- 对每一张图像,使用 SIFT、SURF、ORB 等算法提取特征点,并计算特征描述子。
- 对相邻的图像,使用 KNN、FLANN 等算法进行特征匹配,筛选出满足一致性和稳定性的匹配对。
- 对匹配的特征点,使用 RANSAC、LMedS 等算法进行异常值剔除,提高匹配的准确性。
- 对匹配的特征点,使用多视图几何的约束,如基础矩阵、本质矩阵、单应矩阵等,进行相机位姿的估计,以及三维坐标点的三角化。
- 对估计的相机位姿和三维坐标点,使用 BA(Bundle Adjustment)等算法进行优化,以减少重投影误差和累积误差。
Model parameter
每个高斯椭圆面的参数,包括
- 中心点坐标:(x,y,z)
- 椭球形状shape(使用协方差矩阵∑表示旋转偏移等,∣∑∣越大,椭圆形状越大),使用旋转矩阵和缩放矩阵表示∑=RSSTRT:其中,
- 旋转矩阵R使用旋转四元数q表示 q=qr+qi⋅i+qj⋅j+qk⋅k,
- 缩放变量S即一个列向量S=(sx,sy,sz)T
R=20.5−(qj2+qk2)(qiqj+qrqk)(qiqk−qrqj)(qiqj−qrqk)0.5−(qi2+qk2)(qjqk+qrqi)(qiqk+qrqj)(qjqk−qrqi)0.5−(qi2+qj2)
- RGB三个通道,每个通道使用四阶球谐函数(Spherical Harmonics,SH)表示颜色(可获得比较平滑的连续的颜色变化),因此每个通道有16个待学习参数,表示为C
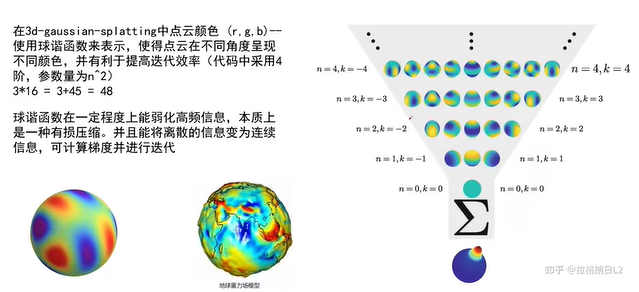
Projection
将点云投影到对应的成像平面,获得投影后的新不透明度α^,以及椭球投影到平面后的形状∑^,用于光栅化渲染
- W为transform过程的世界空间到相机空间的仿射变换(外参):推理时只要获取对应novel view的外参矩阵,就能获得render的image
- J为相机空间到图像空间的变换(内参)s=ϕ(c)的雅可比矩阵,是EWA splatting里提出一种办法,他们称其为“local affine approximation”,可以作线性近似,进行二阶泰勒展开,出现的雅可比矩阵会自然的提供一个线性变换
W=[R03TX01]c=(xc,yc,zc)Ts=(xs,ys,zs)T∑^=JW∑WTJTs=ϕ(c)=(xc/zc,yc/zc,∣∣(xc,yc,zc)∣∣)TJ=∂xc∂xs∂xc∂ys∂xc∂zs∂yc∂xs∂yc∂ys∂yc∂zs∂zc∂xs∂zc∂ys∂zc∂zs=1/zc0xc/∣∣c∣∣01/zcyc/∣∣c∣∣−xc/zc2−yc/zc2zc/∣∣c∣∣α^=α×exp[−0.5⋅(Vs−V0)T∑^−1(Vs−V0)]Vs=(xs,ys)T, V0=(x0,y0)T Rasterization
Tile
通过分块的方式加速渲染,而不是检索每个图像空间的像素级别
- 识别出哪些砖块与特定的高斯投影相交,
- 考虑到一个高斯投影可能会覆盖多个砖块,一种有效的处理方式是复制这个东西,并为每个复制出的高斯分配一个唯一的标识符
- 通过这种方式,3DGS 能有效地降低计算复杂度,同时还保持了图像处理的效率和准确性。
排序 & alpha blending
- 给定像素位置x,通过视图变换W,计算与所有重叠高斯体的距离,即这些高斯体的深度,并从大到小排序,共包含N个椭球,越远的椭球重要性越低,累乘的衰减越多
- 进行Alpha Blending,计算整体图像每个像素点的最终颜色:
C=i∈N∑(ciα^ij=1∏i−i(1−α^j))
raster_settings = GaussianRasterizationSettings(
image_height=int(viewpoint_camera.image_height),
image_width=int(viewpoint_camera.image_width),
tanfovx=tanfovx,
tanfovy=tanfovy,
bg=bg_color,
scale_modifier=scaling_modifier,
viewmatrix=viewpoint_camera.world_view_transform,
projmatrix=viewpoint_camera.full_proj_transform,
sh_degree=pc.active_sh_degree,
campos=viewpoint_camera.camera_center,
prefiltered=False,
debug=pipe.debug
) # 每张图片分别渲染
self._xyz = nn.Parameter(torch.tensor(xyz, dtype=torch.float, device="cuda").requires_grad_(True))
self._features_dc = nn.Parameter(torch.tensor(features_dc, dtype=torch.float, device="cuda").transpose(1, 2).contiguous().requires_grad_(True))
self._features_rest = nn.Parameter(torch.tensor(features_extra, dtype=torch.float, device="cuda").transpose(1, 2).contiguous().requires_grad_(True))
self._opacity = nn.Parameter(torch.tensor(opacities, dtype=torch.float, device="cuda").requires_grad_(True))
self._scaling = nn.Parameter(torch.tensor(scales, dtype=torch.float, device="cuda").requires_grad_(True))
self._rotation = nn.Parameter(torch.tensor(rots, dtype=torch.float, device="cuda").requires_grad_(True))
(超详细!)计算机图形学 入门篇 1. 变换矩阵
本节内容主要是图像变换所对应的矩阵操作,图像的变换操作都可以视作其对应点与变换矩阵相乘所得到的变换结果。课程资料来源于《Fundamentals of Computer Graphics》以及闫老师的GAMES 101课程 GAMES101: 现代计…

https://zhuanlan.zhihu.com/p/448115462

自适应密度控制
- 点密集化:针对在视图空间中具有较大位置梯度(即超过特定阈值)的高斯,克隆小高斯或在过度重建的区域分裂大高斯。这一步旨在于 3D 空间中寻求高斯的最佳分布和表示,增强重建的整体质量。
- 对于分裂,用两个较小的高斯替换一个大高斯,按照特定因子减小它们的尺度
- 点的剪枝:
- 移除冗余或影响较小的高斯,可以在某种程度上看作是一种正则化过程。
- 一般消除几乎是透明的高斯(α低于指定阈值)和在世界空间或视图空间中过大的高斯。
Loss
Combination of L1 loss (absolute of MAE) and D-SSIM(structural similarity index measure) loss,结构相似性
L=(1−λ)L1+λLSSIMλ=0.2 def _ssim(img1, img2, window, window_size, channel, size_average=True) : # gaussian kernel window
mu1 = F.conv2d(img1, window, padding=window_size // 2, groups=channel)
mu2 = F.conv2d(img2, window, padding=window_size // 2, groups=channel)
mu1_sq = mu1.pow(2)
mu2_sq = mu2.pow(2)
mu1_mu2 = mu1 * mu2
sigma1_sq = F.conv2d(img1 * img1, window, padding=window_size // 2, groups=channel) - mu1_sq
sigma2_sq = F.conv2d(img2 * img2, window, padding=window_size // 2, groups=channel) - mu2_sq
sigma12 = F.conv2d(img1 * img2, window, padding=window_size // 2, groups=channel) - mu1_mu2
C1 = 0.01 ** 2
C2 = 0.03 ** 2
ssim_map = ((2 * mu1_mu2 + C1) * (2 * sigma12 + C2)) / ((mu1_sq + mu2_sq + C1) * (sigma1_sq + sigma2_sq + C2))
if size_average:
return ssim_map.mean()
else:
return ssim_map.mean(1).mean(1).mean(1)
SSIM (Structure Similarity Index Measure) 结构衡量指标+代码
SSIM (Structure Similarity Index Measure) 结构衡量指标+代码介绍结构相似指标可以衡量图片的失真程度,也可以衡量两张图片的相似程度。与MSE和PSNR衡量绝对误差不同,SSIM是感知模型,即更符合人眼的直观感受。…

https://zhuanlan.zhihu.com/p/399215180
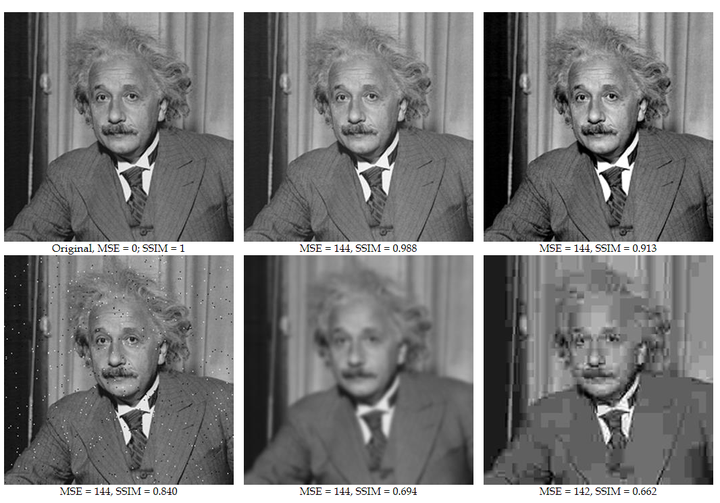
Optimizer
train: Adam
Evaluation: EMA
一句话总结权重滑动平均(Exponential Moving Average)就是:Copy一份模型所有权重(记为Weights)的备份(记为EMA_weights),训练过程中每次更新权重时同时也对EMA_weights进行滑动平均更新,训练阶段结束后用EMA_weights替换模型权重进行预测。
具体地,EMA的超参decay一般设为接近1的数,从而保证每次EMA_weights的更新都很稳定。每batch更新流程为:
Weights=Weights+LR*Grad; (模型正常的梯度下降)
EMA_weights=EMA_weights*decay+(1-decay)*Weights; (根据新weight更新EMA_weights)
应用领域
- SLAM(Simultaneous localization and mapping)即同时定位与建图,它根据对环境的局部观察构建环境全局模型。
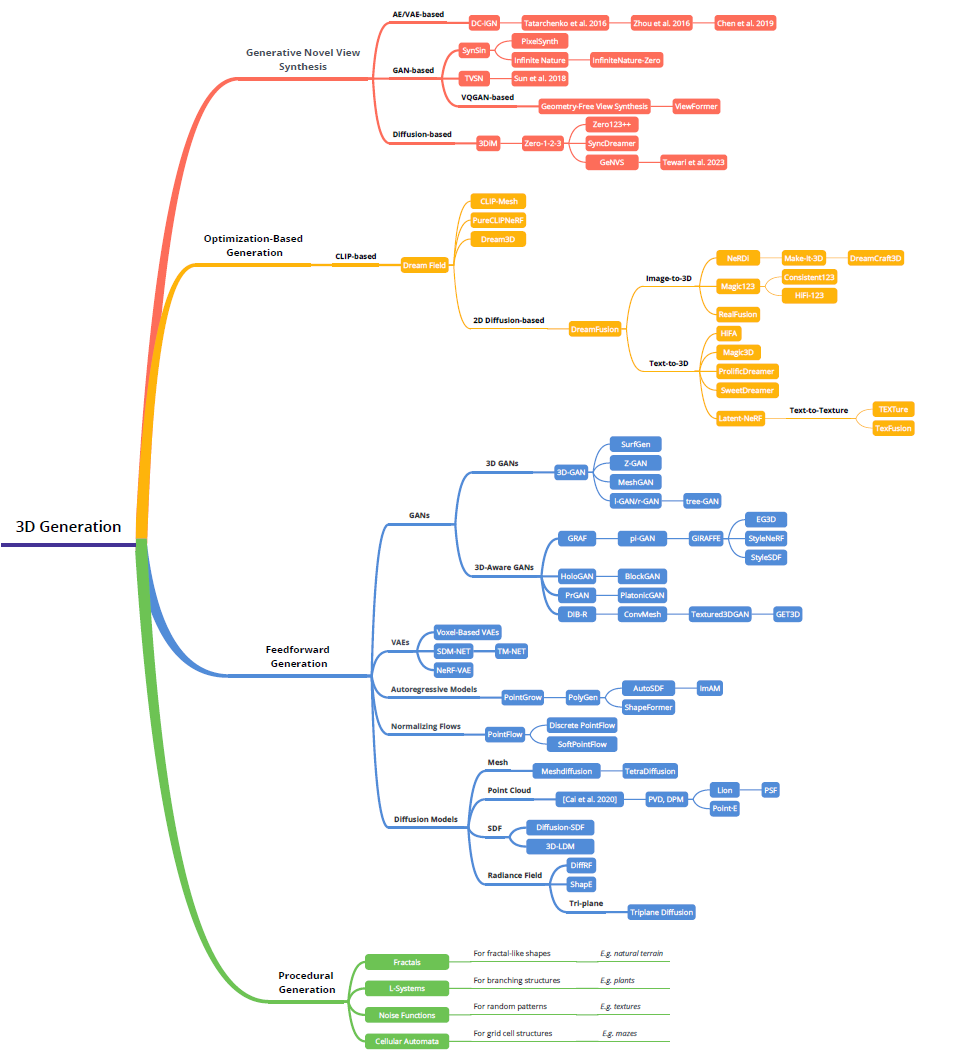
 https://arxiv.org/abs/2401.03890
https://arxiv.org/abs/2401.03890
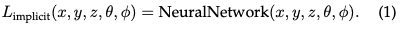
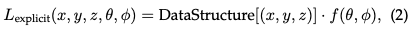
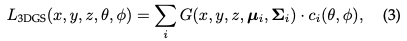



 https://zhuanlan.zhihu.com/p/666465701
https://zhuanlan.zhihu.com/p/666465701
 https://zhuanlan.zhihu.com/p/680669616
https://zhuanlan.zhihu.com/p/680669616
 https://zhuanlan.zhihu.com/p/90295867
https://zhuanlan.zhihu.com/p/90295867
 https://zhuanlan.zhihu.com/p/448115462
https://zhuanlan.zhihu.com/p/448115462
 https://zhuanlan.zhihu.com/p/399215180
https://zhuanlan.zhihu.com/p/399215180