Fused Kernel

💡

Softmax 的优化方法也适用于 LayerNorm，LayerNorm 的数据也可以表示为 (num_rows, num_cols)，计算过程中对每一行的元素做 Reduce 操作求均值方差。减少对global memory的访问次数

LayerNorm

💡

transformer的layernorm计算维度：Hidden size维度

众多框架均对算子做了优化，如：

NVIDIA Apex

Pytorch

OneFlow

LayerNorm 计算方法

以 PyTorch 为例，LayerNorm 的接口为:

torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)

其中 input 形状为：[∗, normalized_shape[0], normalized_shape[1], …,normalized_shape[−1]]

第一个参数 normalized_shape 只能是输入 x_shape 的后几维，例如 x_shape 为 (N, C, H, W), normalized_shape 可以是 (W)， (H, W) ，(C, H, W) 或 (N, C, H, W)。输入 x 在 normalized_shape 这几维上求均值和方差。

第三个参数 elementwise_affine 代表是否要对 normalize 的结果做变换，即 normalize 的结果乘 gamma，加 beta。若 elementwise_affine=True，就多了两个模型参数 gamma 和beta，形状为 normalized_shape。

💡

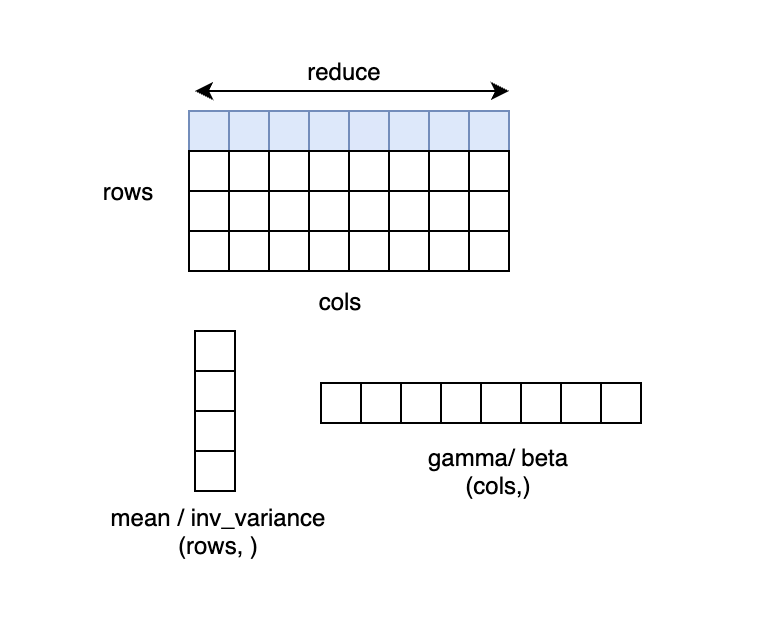
例如对于输入 x 形状为 (N, C, H, W)， normalized_shape 为 (H, W) 的情况，可以理解为输入 x 为 (N*C, H*W)，在 N*C 个行上，每行有 H*W 个元素，对每行的元素求均值和方差，得到 N*C 个 mean 和 inv_variance，再对输入按如下 LayerNorm 的计算公式计算得到 y。若 elementwise_affine=True(default) ，则有 H*W 个 gamma（weight） 和 beta(bias)，对每行 H*W 个的元素做变换。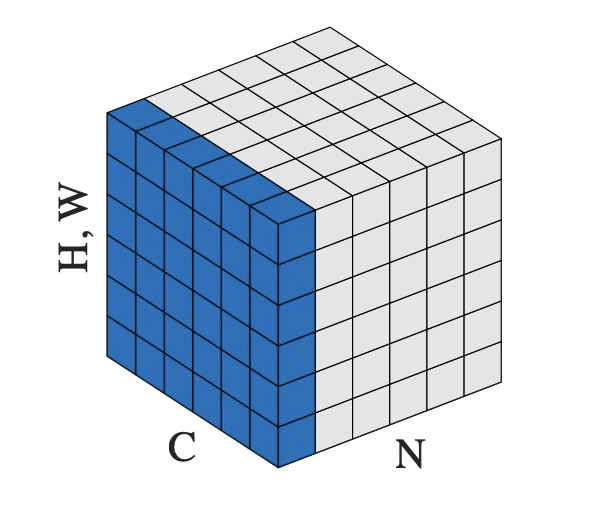

y=\frac {x-E[x]}{\sqrt {Var[x]+\epsilon}}*\gamma + \beta

LayerNorm 中求方差的方法

常见的求方差的方法有 two pass 方法、naive 方法、和 Welford 算法，本文摘录一些关键的公式和结论，详细的介绍和推导可参考：Wiki: Algorithms for calculating variance ，和 GiantPandaCV: 用Welford算法实现LN的方差更新

two-pass方法

使用的公式是：

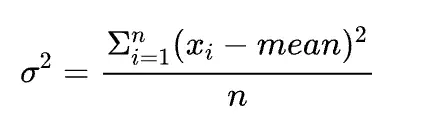
two-pass 是指这种方法需要遍历两遍数据，第一遍累加 x 得到均值，第二遍用上面公式计算得到方差。这种方法在 n 比较小时仍然是数值稳定的。

naive方法

使用的公式是：

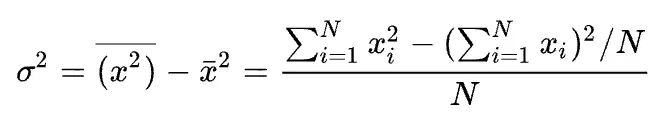
这种方法是一种 single pass 方法，在计算方差时只需要遍历一遍数据累加 x 的平方及累加 x，最后按上述公式计算得到方差。这种方法只需要遍历一遍数据，相比 two-pass 的算法，更容易达到好的性能，但是上面的 Wiki 参考链接中介绍由于 SumSquare 和 (Sum×Sum)/n 可能非常接近，可能会导致计算结果损失精度较大，因此这种方法不建议在实践中使用。

Welford 算法使用的公式是：

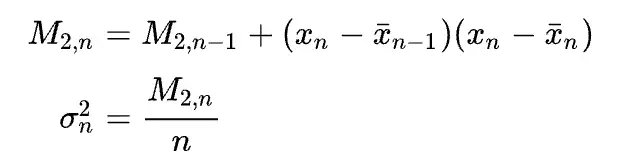
Welford 算法也是一种 single pass 方法(计算均值和方差时只需要遍历一遍数据)，且数值稳定性很好（n比较小时），因此现在很多框架都采用这种方法。本文的代码中采用的也是 Welford 方法。

优化计算

背景：transformer中通常对最后一维计算normalization

base：向量化访存VMA，单次instruction以更高的bits精度访问和存储数据，提高 CUDA Kernel 性能，很多 CUDA Kernel 都是bandwidth bound的，使用VMA可以减少总的指令数，减少延迟，提高带宽利用率。
load and store data but do so in 64- or 128-bit widths. Using vectorized loads reduces the total number of instructions, reduces latency, and improves bandwidth utilization.

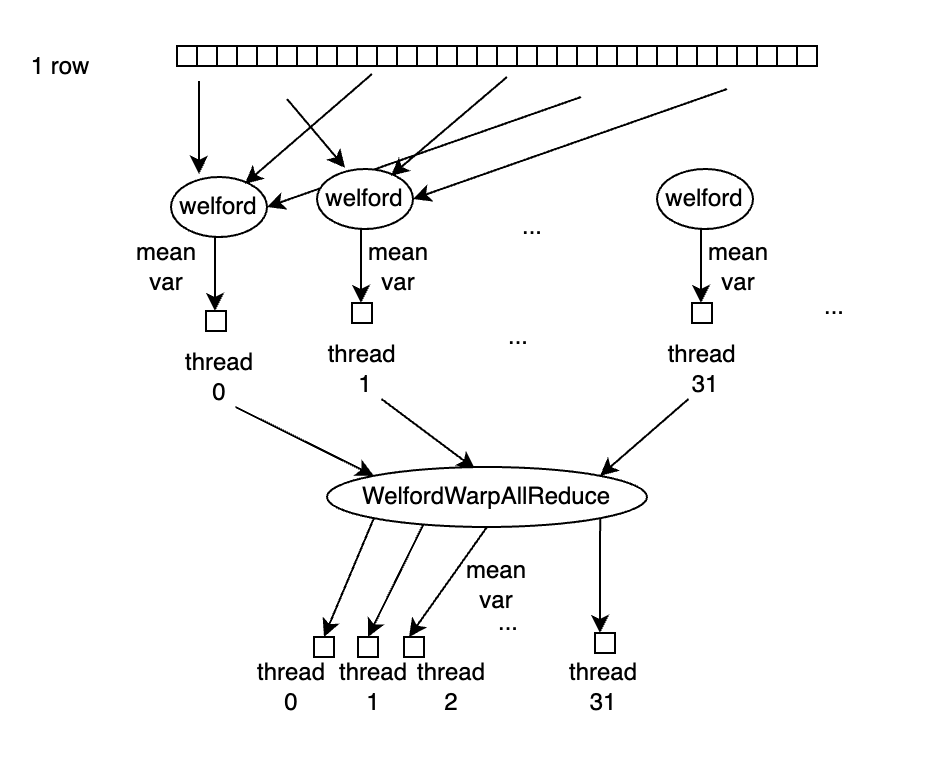
当normalized shape/hidden size不大时，充分利用shared memory保存中间的allreduce结果；根据n_col的大小决定以warp还是block为单位计算均值和方差；通过一次allreduce更新所有thread的计算结果。

使用single pass的Welford 算法计算均值和方差，减少数据遍历次数，且数值稳定性很好

Softmax

尽管当Softmax和CrossEntropy联合使用时，其数学推导可以约简，简化计算

但还是有很多场景会单独使用Softmax Op，如计算attention map时

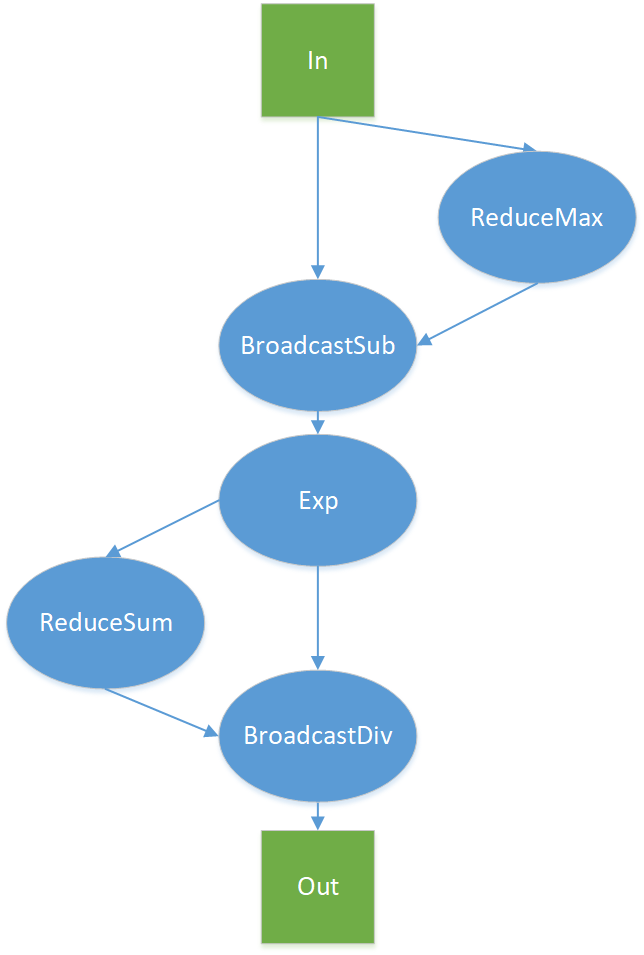
Naive Softmax （注：先减最大值，防止梯度爆炸？）：

先做一个 ReduceMax 求最大值操作，得到输入每一行的最大值；

然后做一个 BroadcastSub 减法操作，拿输入每一行的各点减去每一行的最大值，即常见的softmax表达式中的输入x;

然后做一个自然指数 Exp 操作，对输入每一行的各点计算指数;

然后做一个 ReduceSum 求和操作，对输入每一行的所有结果求和，得到前面公式定义的 ;

最后做一个 BroadcastDiv 除法操作，拿输入每一行的各点的输出；

假设输入的数据大小为D，shape = (num_rows, num_cols), 即 D = num_rows * num_cols，最Navie的操作会多次访问Global memory，其中：

ReduceMax = D + num_rows （read 为 D， write 为 num_rows）

BroadcaseSub = 2 * D + num_rows （read 为 D + num_rows，write 为 D）

Exp = 2 * D （read 、write 均为D）

ReduceSum = D + num_rows（read 为 D， write 为 num_rows）

BroadcastDive = 2 * D + num_rows （read 为 D + num_rows， write 为 D）

总共需要8 * D + 4 * num_rows 的访存开销。由于num_rows相比于D可以忽略，则Navie版本的Softmax CUDA Kernel需要访问至少8倍数据的显存，即： $$ Naive Softmax Kernel 有效显存带宽 < 理论带宽 / 8 $$ 对于GeForce RTX™ 3090显卡，其理论带宽上限为936GB/s，那么Navie版本的Softmax CUDA Kernel利用显存带宽的上界就是936 / 8 = 117 GB/s。

OneFlow实现

与LayerNorm，核心思想一致，如何更高效的处理行计算，分段对 softmax 进行优化：

(1) 一个 Warp 处理一行的计算，适用于 num_cols <= 1024 情况

(2) 当num_cols中等时，一个 Block 处理一行的计算，借助 Shared Memory 保存中间结果数据，1024 < num_cols <= 4096

(3) 当num_col很大时，一个 Block 处理一行的计算，不使用 Shared Memory，重复读输入 x

(4) 向量化访存

Pytorch实现

与OneFlow的前两种一致，分别对应cunn_SoftMaxForward，和softmax_warp_forward；

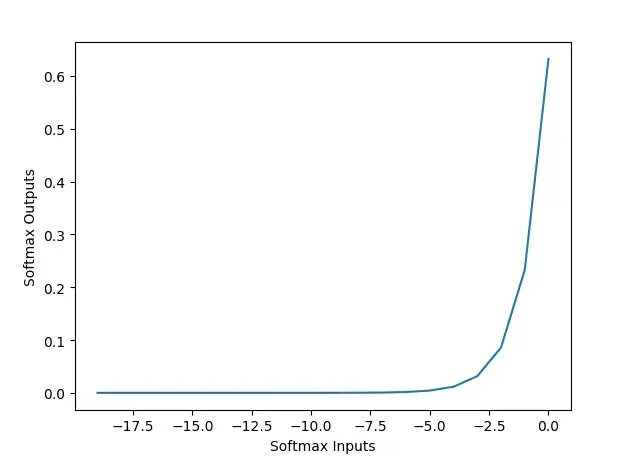
Bias_GeLU

不同的框架对激活函数的实现可能不完全一样，主要原因是从优化前向反向计算量与复杂度、优化内存访问频率的带宽利用率、提升数值计算结果稳定性角度考虑。

例如，GeLU的实现：

原始：
$GELU(x)=0.5*x*(1+Tanh(\sqrt{2/\pi}*(x+0.044715*x^3)))$

BERT：

GELU(x)=0.5*x*(1+torch.erf(x/\sqrt 2))\\ torch.erf(x)=\frac {2} {\sqrt {\pi}}\int_0^x e^{-t^2}dt

与Layernorm和softmax，也是涉及在高维的hidden size维度求指数、求和的操作，fused kernel思路一致。

根据维度选择不同的并行粒度计算

利用shared memory提高访存速度