目录

Compute complexity of self-attention

1. Compute complexity of matrix multiplication

If A, B are n × n matrices over a field, then their product AB is also an n × n matrix over that field, defined entrywise as

1.1 Schoolbook algorithm

The simplest approach to computing the product of two n × n matrices A and B is to compute the arithmetic expressions coming from the definition of matrix multiplication. In pseudocode:

1
input A and B, both n by n matrices
2
initialize C to be an n by n matrix of all zeros
3
for i from 1 to n:
4
    for j from 1 to n:
5
        for k from 1 to n:
6
            C[i][j] = C[i][j] + A[i][k]*B[k][j]
7
output C (as A*B)

This algorithm requires, in the worst case, $n^3$$n^3$ multiplications of scalars and $n^3-n^2$$n^3-n^2$ additions for computing the product of two square n×n matrices. Its computational complexity is therefore $\mathrm{O}(n^3)$$\Omicron(n^3)$

Surprisingly, algorithms exist that provide better running times than this straightforward "schoolbook algorithm". The first to be discovered was Strassen's algorithm, devised by Volker Strassen in 1969 and often referred to as "fast matrix multiplication".[1] The optimal number of field operations needed to multiply two square n × n matrices up to constant factors is still unknown. This is a major open question in theoretical computer science.

As of December 2020, the matrix multiplication algorithm with best asymptotic complexity runs in $\mathrm{O}(n^{2.3728596})$$\Omicron(n^{2.3728596})$time, given by Josh Alman and Virginia Vassilevska Williams.

1.2 Strassen's algorithm

Strassen's algorithm improves on naive matrix multiplication through a divide-and-conquer approach. The key observation is that multiplying two 2 × 2 matrices can be done with only 7 multiplications, instead of the usual 8 (at the expense of several additional addition and subtraction operations). This means that, treating the input n×n matrices as block 2 × 2 matrices, the task of multiplying n×n matrices can be reduced to 7 subproblems of multiplying n/2×n/2 matrices. Applying this recursively gives an algorithm needing $\mathrm{O}(n^{lo{g}_{2}7})\approx \mathrm{O}(n^{2.807})$$\Omicron(n^{log_27})\approx \Omicron(n^{2.807})$ field operations.

Unlike algorithms with faster asymptotic complexity, Strassen's algorithm is used in practice. The numerical stability is reduced compared to the naive algorithm, but it is faster in cases where n > 100 or so and appears in several libraries, such as BLAS. It is very useful for large matrices over exact domains such as finite fields, where numerical stability is not an issue.

2. Compute complexity in self-attention

2.1 Definition of self-attention

In this blog, self-attention layer consists of a point-wise feed-forward computation and self-attention function. The compute complexity of transformer claimed in Transformer Paper contains only self-attention function.

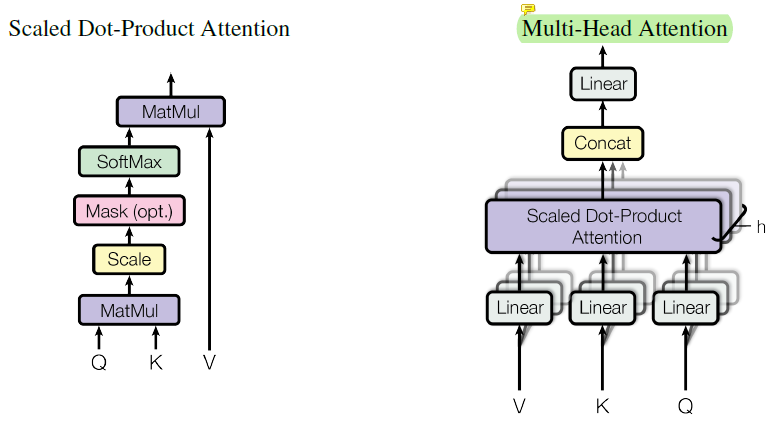
2.2 Complexity calculations

Assuming $X$$X$ is the input of self-attention, whose shape is $(n,d)$$(n,d)$, where $n,k$$n, k$ represent number of tokens and dimension of each token, respectively.

• Point-wise feed-forward computation: Linear computation to obtain $Q,K,V$$Q,K,V$, eg. $Q^{\mathbb{R}(n,d)}=X^{\mathbb{R}(n,d)}{W}_Q^{\mathbb{R}(d,d)}$$Q^{\Bbb R(n,d)}=X^{\Bbb R(n,d)}W_{Q}^{\Bbb R(d,d)}$, whose compute complexity is $\mathrm{O}(n{d}^2)$$\Omicron(nd^2)$

• Self-attention function: $Attention(Q,K,V)=softmax(\frac{Q{K}^T}{{\sqrt{d}}_k})V$$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt d_k})V$. Computing $Q{K}^T$$QK^T$ (multiple reshape operation) has complexity $\mathrm{O}(n^{2}d)$$\Omicron(n^2d)$, and post-multiplying the result with $V$$V$ has complexity $\mathrm{O}(n^{2}d)$$\Omicron(n^2d)$ as well. Hence the compute complexity is $\mathrm{O}(n^{2}d)$$\Omicron(n^2d)$

Therefore, the total complexity of the layer is $\mathrm{O}(n{d}^2+n^{2}d)$$\Omicron(nd^2+n^2d)$. BUT!!, as mentioned above, the claimed compute complexity in paper is only the self-attention function, while point-wise feed-forward complexity is not included.

So in Table 1 is strictly the attention mechanism, it is not the complexity of the Transformer. Authors are very well aware about the complexity of their model (I quote):

Separable convolutions [6], however, decrease the complexity considerably, to O(k·n·d + n·d^2). Even with k = n, however, the complexity of a separable convolution is equal to the combination of a self-attention layer and a point-wise feed-forward layer, the approach we take in our model.

3. Personal view

Quote:

Now, to understand what Table 1 contains please keep in mind how most people scan papers: they read title, abstract, then look at figures and tables. Only then if the results were interesting, they read the paper more thoroughly. So, the main idea of the Attention is all you need paper was to replace the RNN layers completely with attention mechanism in seq2seq setting because RNNs were really slow to train. If you look at the Table 1 in this context, you see that it compares RNN, CNN and Attention and highlights the motivation for the paper: using Attention should have been beneficial over RNNs and CNNs. It should have been advantageous in 3 aspects: constant amount of calculation steps, constant amount of operations and lower computational complexity for usual Google setting, where n ~= 100 and d ~= 1000.